圆周率的计算过程,经历了实验算法、几何算法、分析算法和计算机算法的过程;其中,新工具的出现,对计算圆周率起了重要作用。
实验算法
在古时候,人们对圆周率的精度要求还不高。比如公元前1世纪左右,我国最古老的数学著作《周髀算经》,就记载着“径一周三”,也就是把圆周率近似看作“3”。
在古巴比伦时期(公元前1900年~公元前1600年),古巴比伦人就记载了圆周率=25/8=3.125。
古人只需要画一个圆,然后分别测量其周长和直径,就可以得到圆周率;虽然和圆周率的真实数值相差很大,但是对那时候的生产活动来说足够用了。
但该方法对圆周率的计算精度非常有限,只能精确到圆周率的小数点后第一位,要想精确到第二位都很困难。
几何算法
几何算法避免了测量的误差,比如阿基米德(公元前287~212),计算圆的内切正多边形和外接正多边形,然后取其平均值,把圆周率计算到3.141851。

圆周率有几种算法?圆周率的计算经历了的过程
而我国的古代数学家祖冲之(429~500),利用割圆术,计算到正24576边形,把圆周率精确到小数点后第七位(3.1415926~3.1415927),这一记录保持了800多年才被欧洲人打破。
15世纪,阿拉伯数学家卡西,把圆周率精确到17位小数。
1596年,德国数学家鲁道夫·范·科伊伦,把圆周率精确到20位小数。
1610年,鲁道夫·范·科伊伦耗尽毕生精力,用了10多年的时间,再次把圆周率精确到了35位,这也算是手工几何算法的极限了。
分析算法
进入18世纪后,数学家有了三角函数、连分数、无穷级数、微积分和虚数等工具,大量圆周率的计算公式涌现出来,大大提高了数学家计算圆周率的效率。
比如著名的梅钦公式:

圆周率有几种算法?圆周率的计算经历了的过程
由英国数学家梅钦,于1706年提出,该级数的收敛速度非常快,至今也是计算机计算圆周率的主要公式之一。
数学家Jurij Vega,在1789年,利用梅钦公式把圆周率精确到140位小数(后来得知前137位才是正确的)。
人工计算的记录,是在1948年,美国两位数学家利用一个全新的圆周率公式,手工计算到了808位小数。
比如我们利用虚数i的性质,可以轻松构造出许多圆周率的级数:

圆周率有几种算法?圆周率的计算经历了的过程
还有印度数学奇才拉马努金,仅凭冥想就能意会出许多圆周率级数,而且级数的收敛速度非常快,比如下面两个公式就是拉马努金提出来的:
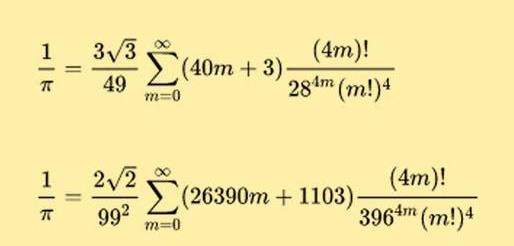
圆周率有几种算法?圆周率的计算经历了的过程
其中第二个公式,只要输入第一项,就可以把圆周率精确到十进制的第八位:
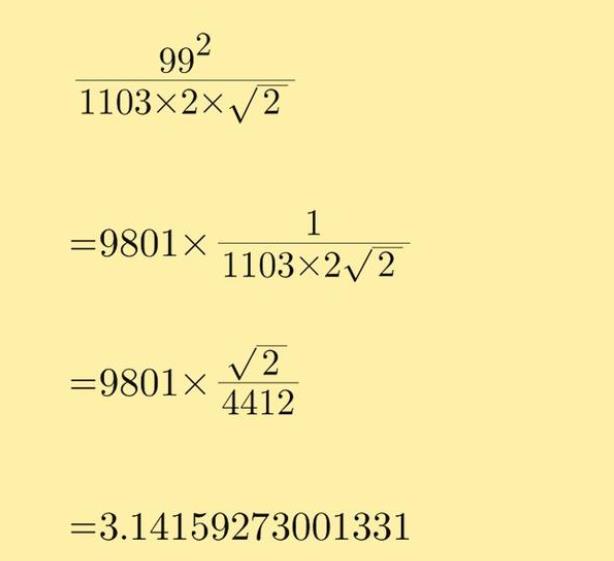
圆周率有几种算法?圆周率的计算经历了的过程