长方形和正方形
今天开始几何图形类的分享,一般从三年级开始接触图形,第一个知识点就是长方形和正方形,据说也是小升初的重点题型。学习图形我们首先要学会画图分析,其次要记住相关的公式,例如正方形的相关公式:边长乘以边长=面积;边长乘以4=周长。长方形的相关公式:(长+宽)×2=周长;长乘以宽=面积。除此以外,还会向大家介绍求周长面积的一些技巧,通过细心观察,把握图形特点,合理进行切拼,通过平移法,标向法,填补法等方法巧求周长和面积。欢迎继续关注我的文章,每天都为大家带来数学思维的分享。
长方形与正方形周长——公式类
解析:这类题型较为简单,首先就是要记住相关的公式,正方形的周长=边长乘以4,长方形的周长=(长+宽)×2
例题1:一个长方形和一个正方形,周长相等。已知正方形的边长是36厘米,长方形的长是宽的2倍,求这个长方形的长和宽各是多少厘米。
解析:通过第一句话两个图形的周长相等,如果能求出正方形的周长即能得出长方形的周长。

正方形的周长=边长36×4=144厘米
144厘米也是长方形的周长

长方形的周长144厘米=(长+宽)×2
那么长+宽=144÷2=72厘米
条件说了长方形的长是宽的2倍,长宽的和为72厘米,这是不是简单的和倍问题了。遇到和倍问题,我们就画线段图:

把宽假设为1份,那么长就是2份,加起来为3份,对应的数字是72厘米,那么一份也就是宽=72÷3=24厘米,长=24×2=48厘米。
例题2:用6张边长为2厘米的正方形纸片拼成一个长方形,这个长方形的周长是多少厘米?
解析:首先我们来画图

通过图形,我们很容易看出来,新组合的长方形,长为2×3=6厘米
宽为2×2=4厘米,然后根据公式:周长=( 长+宽)×2,得出长方形的周长为(6+4)×2=20厘米。那这是不是唯一答案呢?其实还有另外一种画法:

显而易见,这个长方形的长为12厘米,宽为2厘米,所以周长为(12+2)×2=28厘米
例题3:把长108厘米的铁丝围城一个长方形,使长比宽多12厘米,求长宽各是多少?

通过公式长方形周长=(长+宽)×2,得出长+宽=108÷2=54厘米
条件告诉我们长比宽多12厘米,那么这就是一个简单的和差问题,遇到和差问题,画线段图:

我们把宽看成1份,那么长就是1份+12厘米,我们用54-12=42厘米,就是两份宽,一份数也就是宽为21厘米,长就是21+12=33厘米。
长方形与正方形题型二:巧求周长
方法一:等量代换(用一种量来代替和它相等的另一种量,我们就来探讨一下如何运用在题目中)
例题1:如图,5个相同的小长方形拼成一个大正方形。已知大正方形的周长比小长方形的周长多10厘米。那么小长方形的周长是多少?

解析:已知大正方形的周长比小长方形的周长多10厘米,首先我们要找出这10厘米对应的是什么?通过图形我们可以看出,小长方形的两条长与正方形的两条边长是相等的,多出来的就是这8条线段,一条线段相当于一条小长方形的宽,所以8×宽=10厘米,得出宽=1.25厘米。
观察图形可知,因为小长方形的长与正方形的边长是相等的,所以小长方形的长=5倍宽。找到长宽的关系,这时我们就可以进行等量代换。通过公式小长方形的周长=(长+宽)×2,将长换成5宽,那么换算过来就是12宽=周长,得出小长方形周长=12×1.25=15厘米。
例题2:如图,在长方形ABCD中,EFGH是正方形。如果AF=16厘米,HC=21厘米,那么长方形ABCD的周长是多少?
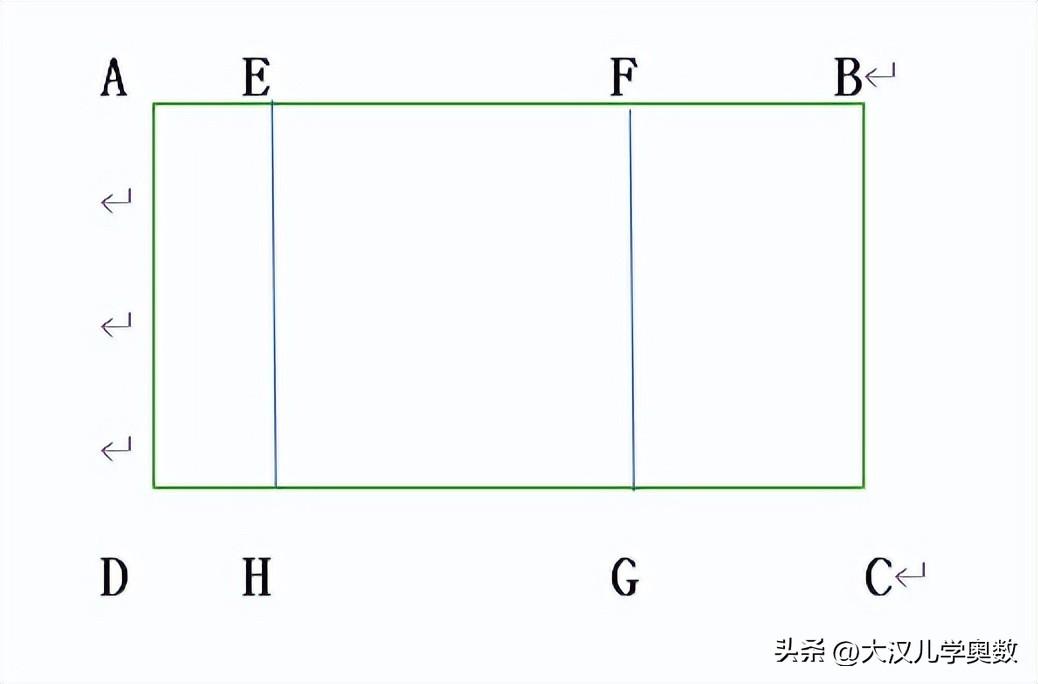
长方形的宽为BC,长为DH+HG+GC,由公式周长=(长+宽)×2,推出周长=(BC+DH+HG+GC)×2.我们用等量代换的方法来解题,看看哪些量是相等的呢?已知HC=21厘米=HG+GC=FG+GC=BC+GC,DH+HG=AF=16厘米 最后得出答案ABCD的周长=(21+16)×2=74厘米。
例题3:如图,在长方形ABCD中,AB=14厘米,AD=12厘米,现沿其对角线BD将它对折,得一几何图形,则图中阴影部分周长是多少厘米?

阴影部分得周长=A’D+A’F+DF+FC+CB+BF 那么哪些量可以等量代换呢。A’D=AD=12厘米 DF+FC=DC=AB=14厘米 A’F+BF=A’B=AB=14厘米 CB=AD=12厘米
得出阴影部分的周长=12+12+14+14=52厘米
用平移法巧求图形周长
解析:计算面积时,可以将图形进行平移,将不规则图形变为规则图形。
例题1:下面图形的周长为多少厘米?

通过这些线段的平移,我们得到一个规则的长方形。这个长方形的宽为4厘米,长为8厘米。根据公式:长方形的周长=(长+宽)×2,得出周长为(4+8)×2=24厘米。
根据平移法原理衍生出了一种新的方法叫标向法,先确定一个点,再按一个方向标向。可以得出可知向下线段之和=向上线段之和;向左线段之和=向右线段之和。周长=向上(下)线段之和×2+向左(右)线段之和×2.标向法多用于不规则图形。你觉得哪个方法更简单呢?
例题 2:下图的周长是多少?

通过平移如图,这个不规则图形周长等于大长方形加上AB、CD的长,即周长=(50+35)×2+10×2=190厘米。
用标向法巧求不规则图形周长
解析:在线段上标出方向(常用于凹多边形),可知向下线段之和=向上线段之和;向左线段之和=向右线段之和。周长=向上(下)线段之和×2+向左(右)线段之和×2.
例题1:根据条件,求下面图形的周长。

由图可知,向左总长度=向右总长度=10厘米;向上总长度=向下总长度=6+2+4=12厘米,周长由上下左右四个方向的总长度组成,所以周长为10×2+12×2=44厘米
长方形与正方形周长题型三:剪切后求周长
解析:此类题型有个重要的知识点,切一刀,多两边。
例题1:如图,大长方形的长为8厘米,宽为6厘米,将其沿着虚线剪成三个小长方形,这三个小长方形的周长之和为多少厘米?

解析: 我们剪了两刀,增加了4个长,
原长方形的周长为(8+6)×2=28厘米
增加的边长为4×8=32厘米,所以三
个小长方形的周长和为28+32=60厘米
例题2:把长方形横剪一刀、竖剪一刀,剪完后的4个长方形的周长之和是多少?

解题:先看横剪一刀,剪一刀增加了两边,所以变为4条长边,用11×4=44厘米;竖剪一刀,增加了两边,所以就变为4条宽,用7×4=28厘米。再将以上数字相加得到44+28=72厘米
例题3:有一个长方形纸片,长是宽的2倍,周长是36厘米,用剪刀剪5下(如图),这12个长方形的周长之和是多少厘米?

解题:通过第一句话长是宽的2倍,周长是36厘米,根据公式周长=(长+宽)×2求出长+宽=36÷2=18厘米,知道长宽的倍数以及它们的和,这明显是个和倍问题,遇到和倍问题,画线段图。
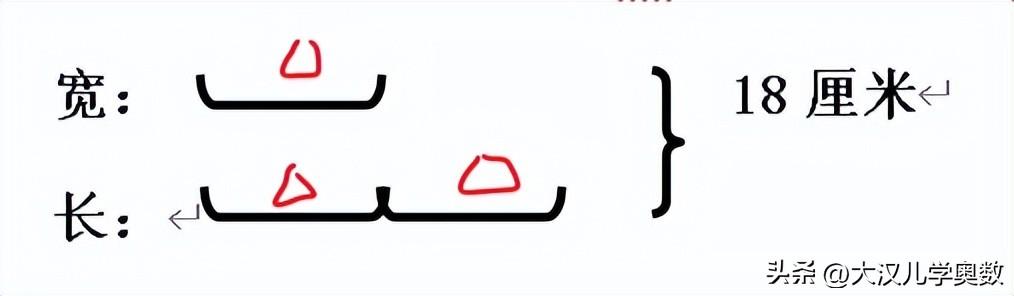
可以看出3倍宽=18厘米,得出宽=6厘米,长就为12厘米
先看横着剪了3刀,剪一刀增加两边,剪3刀就增加了3×2=6边,加上原来的2条长,现在就变成了8条长,用12×8=96厘米。
再来看竖着剪2刀,剪一刀增加两边,剪2刀增加了2×2=4边,加上原来的2条宽,现在就变成了6条宽,用6×6=36厘米。
将得出来得两个数相加,得到这12个长方形的周长之和为96+36=132厘米。
总结:这道题结合了和倍问题,长方形周长公式,剪切后求周长三个知识点,有一定的难度,我们需要把每个知识点都吃透再来解题。
长方形与正方形周长题型四:图形拼合
解析:我们前面讲了图形剪切,剪一刀,增两边。那么反过来拼一次,就少两边。
例题:把两个长6厘米、宽4厘米的长方形沿着长拼成一个大长方形,拼成的大长方形周长是多少厘米?

解题:我们先算两个小长方形的周长,一个小长方形周长为(6+4)×2=20厘米,因为它们长宽相等,两个小长方形周长就为20×2=40厘米。因为是沿着长边拼接,拼一次少两边,就少了两条长,6×2=12厘米。用原来两个小长方形的周长40-12=28厘米,就是拼成的大长方形周长。